When is Weather Really "Climate"?

Answer: when the weather is warm. 

Over at Statistician to the Stars, we find some commentary on a recent calculation that thirteen consecutive months of above-average temperatures has a 1 in 1.6 billion probability of occurring by chance.  This figure was obtained by considering temperature anomalies (deviations of adjusted actual temperatures from the mean temperature for that month), classifying them as "above normal," "normal," and "below normal," and assigning probabilities of 1/3 to each group.  Then taking ⅓^13 to calculate the probability of a run of 13 "above-normal" temperatures.  This is a fairly simplistic model.  It also suggests that 14 months ago, temperatures were normal or below.  You will notice that 13 months is just over one year, which hardly qualifies as climate and may not even qualify as 13 independent measurements. 


Dr. Briggs writes...

... because this probability—the true probability—was so small, ... the Simple Model was false. And that therefore rampant, tipping-point, deadly, grant-inducing, oh-my-this-is-it global climate disruption on a unprecedented scale never heretofore seen was true. That is, because given the Simple Model the probability was small, therefore the Simple Model was false and another model true. The other model is Global Warming.
This is what is known as backward thinking. Or wrong thinking. Or false thinking. Or strange thinking. Or just plain silly thinking: but then scientists, too, get the giggles, and there’s only so long you can compile climate records before going a little stir crazy, so we musn’t be too upset.

Basically, the reasoning was

Pr(13-in-a-row|Simple Model)

Therefore, Warming Model.  

But the Warming Model is not the only alternative model, and for that matter, the Simple Model was only shown to be improbable, not absolutely wrong.  No matter how small p is, pN>0 for sufficiently large N.  IOW, given a long enough data series, improbable events are virtually guaranteed. 

Curiously, a David Fox on the blog Planet 3.0 writes:

Since records began in 1895, there have been 1404 months. This means there are 1391 13-month periods and none of them have exhibited the behavior that we have observed in the most recent 13-month period.

This would indicate an empirical estimate (relative frequency, essentially by jackknifing) of

Pr(13-in-a-row) = 1/1391 (or 0.07%), 

considerably greater than a billionth-and-a-half.  But no one there seems to have noticed that.  Then too, the 1391 periods are mutually correlated to the tune of up to 92%.  That is, two consecutive such intervals will share 12 of their 13 months. 


The estimable Dr. Briggs continues:

Yet there also exists many other rival models besides the Global Warming and Simple Models. We can ask, for each of these Rival Models, what is the probability of seeing 13-in-a-row “above-normal” temperatures? Well, there will be some answer for each. And each of those answers will be true, correct, sans reproche. They will be right [given the model].
Now collect all those different probabilities together—the Simple Model probability, the Global Warming probability, each of the Rival Model probabilities, and so on—and do you know what we have?
A great, whopping pile of nothing. 

 IOW, we have

• Pr(13-in-a-row|Simple Model), 
• Pr(13-in-a-row|Warming Model), 
• Pr(13-in-a-row|Solar Cycle Model), 
• Pr(13-in-a-row|Some Other Model), etc.  

And you cannot tell from the resultant probabilities which one is actually True.  

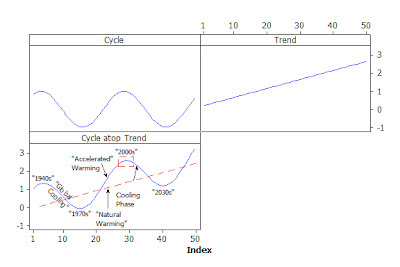
For example: here are three models: a stationary cycle, a linear trend, and a cycle riding atop a trend:

If you take the dotted line box labeled "2000s" and mentally transfer it to the stationary cycle above, you can see how a 13-months-in-a-row series of "above normals" can happen even if there is no trend at all, let alone the 400-year old rebound from the Little Ice Age. 

You can't handle the truth!

An Excursus on Truth and Fact

Ever wonder why those are two different words?  The historian John Lukacs once complained that Americans were always reducing truths to facts.  So what's the diff?

• Fact: from the Latin factum est, the participle of a verb, meaning "that which has the property of having been accomplished."  It is cognate with "feat."  When Jane Austen wrote "gallant in fact as well as word," it still meant "gallant in deeds as well as words."  You can see this clearly in the German term for fact: die Tatsache, lit. deed-matter.
• Truth: from West Saxon triewð or Mercian treowð, meaning "faithfulness," from triewe, treowe "faithful."  Truth is therefore transitive.  One must be true "to" something.  The Beach Boys prophesied "be true to your school," a bricklayer lays a true line of bricks, a husband promises to be true to his wife (which is why they are "be-truthed" (betrothed)). 

To these we may add for slaps and giggles:

• Fiction: from Latin fictio, the "act of shaping or forming."   Since all scientific theories are formed by arranging facts, they are fictions. 

Traditionally, there are two kinds of truth:

• Correspondence or "true to fact."  This is the truth of natural science.  A scientific hypothesis is "true" if it is compatible with all the relevant facts/measurements/data.  It can be overthrown by the discovery of a new fact with which the hypothesis is incompatible. 
• Coherence or "true to a model."  This is the truth of mathematics.  A mathematical theorem is "true" if it is compatible with all other theorems within the chosen system of axioms.  Unlike scientific truths, mathematical truths cannot be overthrown, provided the proof was a valid one. 

This distinction is one reason why mathematics is not natural science.  A lot of atheist-theist arguments stem from confusing these two kinds of truth.

There is truthiness less lofty than the scientific and mathematical truths.  For example, literary fiction is said to be True to Life, which is a form of being True to Fact.  Theological truths, like mathematical ones, are judged by coherence to an entire system of belief and are proven by metaphysical reasoning. 

Not all truths are factual.  Consider "Beauty and the Beast."  It is not a factual account, but it is a true one.  The truth is this: that sometimes a person must be loved before he becomes lovable.  

The Facts of Life

So the statement that Pr(13-in-a-row|Simple Model)=1 in 1.6 billion is a truth more akin to theology than to science.  That is, it is true to a [particular] model.  Assume the model, the calculation follows.  But it does not tell us whether the model is true to life. In fact, the calculation assumes that monthly anomalies constitute white noise. 

Pierre Duhem, physicist and
philosopher

Pierre Duhem pointed out that modus tollens (Popper's famous "falsification," known since Aristotle) must be applied cautiously to physical theories; that is, to true-to-fact statements.  From the Stanford Encyclopedia of Philosophy:

[W]hen there is some conflict with experience what is disconfirmed ["falsified"] is necessarily ambiguous. Duhem's formulation of his non-falsifiability thesis is that “if the predicted phenomenon is not produced, not only is the questioned proposition put into doubt, but also the whole theoretical scaffolding used by the physicist.” He ... says “the only thing the experiment teaches us is that, among all the propositions used to predict the phenomenon and to verify that it has not been produced, there is at least one error; but where the error lies is just what the experiment does not tell us.”  He refers to two possible ways of proceeding when an experiment contradicts the consequences of a theory: a timid scientist might wish to safeguard certain fundamental hypotheses and attempt to complicate matters by invoking various cases of error and multiplying the corrections, while a bolder scientist can resolve to change some of the essential suppositions supporting the entire system. The scientist has no guarantee of success: “If they both succeed in satisfying the requirements of the experiment, each is logically permitted to declare himself content with the work he has accomplished.” 

Thus if a computer climate model were contradicted by a decade-long period of no net increase in temperature, it is not clear what in the model is wrong. 

Modus tollens states:

If P then Q
and Not-Q
Therefore, Not-P

This works well enough in math (and Popper iirc was a mathematician) but Duhem noted that for physical experiments, as for Lays Potato Chips, you can't have just one P.  The better formulation is

If {P1 and P2 and... Pn} then Q
and Not-Q
Therefore, {Not-P1 or Not-P2 or... Not-Pn}

and you can't easily know which P has been falsified. Difficulties ensue when we forget P2 and.., Pn are even there.  [We forego Carnap, who pointed out that there are multiple Qs.]  Consider three famous falsifications.

• Heliocentrism (P) cannot be true because it predicts visible parallax (Q) and no visible parallax can be found.  But "P2" was "the fixed stars" are at most 100x the distance of Saturn."  This in turn was based on the assumption that Airy disks were real and that stars reflected sunlight.  The lack of visible parallax was due to the stars being much farther than their apparent diameters and brightnesses had indicated.
• Evolution by natural selection (P) cannot be true because a new mutation would be diluted out of the species within the first few generations, unless it appeared simultaneously in most of the population.  But P2 was the assumption that inheritance was a continuous process, a "bloodline," and Gregor Mendel showed that inheritance was a discrete process involving "genes."  Recessive genes were sufficient to answer the objection.
• Maxwell's electromagnetism (P) predicted that all magnetic fields were generated by electricity (Q).  But permanent magnets were not electrified (not-Q), falsifying the theorem.  The hidden P2 was the assumption that there was no electrical motion in a permanent magnet.  An epicycle was proposed -- the electron -- to resolve the problem, and has so far held up reasonably well.

They Do Run-Run-Run; They Do Run-Run

A run is a series of consecutive points on the same side of the median [of all the points in a time series].  Think of a coin toss.  To get H-H-H-H-H-H-H-H-H-H-H-H-H would be considered unlikely.  But so would be H-T-H-H-H-T-T-H-H-H-T-H-T (generated via random number generator on Minitab) or any other specific sequence of H and T.  However, we are typically interested in Events rather than in Outcomes.  An Event is a set of Outcomes that we consider together due to final causes we have in mind.  It is why the four possible royal flushes are regarded with keener interest than the vast number of poker hands consisting of unmatched cards.  A hand consisting of {2H, 5S, 8D, 10C, QH} is no less likely than one consisting of {10H, JH, QH, KH, AH}.  But it is not the Pr(10H, JH, QH, KH, AH) that we find interesting; it is Pr(Royal flush).  That is, the Event consisting of various outcomes, not the single outcome. 

Third edition, with co-authors,
first edition was by Ott alone and
had fewer Greek letters.

In Ellis Ott's Analysis of Runs, applied to time series of industrial processes, six consecutive points on the same side of the median are considered sufficiently interesting to warrant investigation of the process.  Pr(HHHHHH or TTTTTT) is p=0.031; i.e., it is unlikely to happen if the process is stable (constant mean).  This is called the α-risk.  Therefore, when encountered, it justified a root-cause investigation.  (More importantly, when not encountered, it meant keep your cotton-picking fingers off the control panel.) 

But Ott's students and grandstudents were aware that the calculation of this α-risk assumed not only that:

P1) Ho: Δμ = 0; i.e., the process mean is constant.

But also that:

P2) Successive points are independent; i.e., no serial correlation.
P3) The distribution is symmetric.
P4-Pn) Plus other stuff, such as that the measurement system is accurate, precise, linear, stable, etc. 

Thus, an improbable result means that either P1 or P2 or... Pn is unlikely to be true.  For example:

• the process mean μ really has shifted (from some previously determined value).
• the data are serially correlated, e.g., continuous chemical processes, consecutive monthly temperatures.  
• the data are not symmetrically distributed, e.g., sample ranges, trace chemical contents, et al.  
• the measuring system malfunctioned. 

TOF has encountered examples of all of these in his gripping adventures as a quality engineer.  But even if the process mean really has shifted, this analysis does not tell us why it has shifted.  For that, a root cause analysis is required. 


That is, if the constancy of μ is improbable given a particular model, that does not mean any other particular model right.  Like Thomas Aquinas considering the nature of God, all we can say is what μ was not; viz., constant.  There is an infinitude of possible "Alternate Hypotheses."  You can never "prove" an Alternative Hypothesis; you can only reject (with greater or lesser confidence) the Null Hypothesis. 

All probabilities are calculated from a particular model, and if the assumptions of the model are not met, the probability may not be true to life, even though it be true to the model.  For example, if there is serial correlation month-to-month (as we would expect with weather climate) a 13-month run of higher-than-"normal" temperatures could be far more probable than the Simple (white noise) Model suggests. 

For that matter.... what if we took as "normal" the average temperature since the onset of the current interglacial period?  We might never have had a higher-than-"normal" month in all of recent history!