Now the aforesaid article appeared in the Jan/Feb 2013 issue of Analog,
- The article has appeared on-line as part of the reading for a course in science education, taught by Leonard Bliss at Florida International University in Miami. This non-commercial use was with permission.
- For technical reasons having to do with file size, the article was published without the accompanying artwork and diagrams.
(*) You-Know-Who. Galileo. You knew that, right?
1. Our Ancestors Were Stoopid
Before you laugh at your ancestors, TOF invites you to prove that the earth is, contrary to your senses, in wild and careening double motion: spinning like a top and whipping around the sun without (somehow) leaving the Moon and Air behind, and without everyone stumbling around like dunkards. You are not allowed to appeal to authority or to the success of NASA, or suchlike things. You've got eyeballs and armillaries, and that's pretty much it. Go. TOF will wait here.
2. Sundry Proofs of the Stationary Earth
Astonishingly, Late Moderns, who hold heliocentrism as a sort of holy doctrine, are generally unaware of the empirical evidences that would justify it; while Early Moderns, who thought geocentrism dough-face obvious, were well aware of the evidences that falsified heliocentrism. These evidences, plucked variously from Aristotle, Oresme, and Riccoli follow; but be it noted that both Oresme and Riccoli also supplied rebuttals for most of them and Aristotle cautioned against taking his cosmology as more certain than he himself did:"We are far away from the things we are trying to inquire into, not only in place but more so in that we have sensation of exceedingly few of their accidents. .... It is good to inquire about these things and so to deepen our understanding, although we have little to go on and we are situated at such a great distance from the attributes of these things. Nevertheless, from contemplating such things nothing [we infer] should seem to be unreasonable, holding them now as fraught with difficulties. – Aristotle, On the heavens, 2.3.286a5-7 and 2.12.292a14-18
 |
| Fig. 2. Ancient version of Michelson-Morley experiment |
2.1 The Argument of the Winds.
If the Earth is rotating, "we and the trees and houses are moved toward the east very swiftly, and so it should seem that the air and wind blow continuously and strongly from the east, much as it does against a quarrel shot, only much more strongly.…. But the contrary appears by experience." Therefore, the earth does not turn. (Oresme, "On the book of the heavens and the world by Aristotle.") |
| Fig. 3. The Arrow. I shot an arrow into the air. It should fall west, not in my hair. I do not fear it in the least: As the arrow flies, the earth moves east. Or not. Ouch! |
2.2 The Argument of the Arrow.
"If a person is on a ship moved rapidly eastward and an arrow were shot directly upward, it ought not to fall on the ship but a good distance westward from the ship. Similarly, if the earth is moved so swiftly in turning from west to east, and it has been posited that one throws a stone directly above, then it ought to fall, not on the place it left, but a good distance to the west. But in fact the contrary is clear." (Oresme, "On the book of the heavens and the world by Aristotle.")
 |
| Fig. 4. As the world turns. The top of the tower moves faster than the bottom, so objects dropped from the top will have an eastward deflections and fall east of the plumb line. Not to scale, dudes! |
2.3 The Argument from Coriolis
If the Earth is rotating objects at the tops of tall buildings will be moving eastward at a higher velocity than those at the base of the building. Therefore, an object dropped from the top of a tower will fall east of the plumb line. No such deflection is observed. (This argument was unknown to Aristotle and the medievals, but was included in Riccioli's Almagestum novum, summarized by Graney in "126 Arguments Concerning the Motion of the Earth."
2.4. The Argument from Parallax.
"The earth, then, also, whether it move about the center or as stationary at it, must necessarily move with two motions. But if this were so, there would have to be passings and turnings of the fixed stars. Yet no such thing is observed. The same stars always rise and set in the same parts of the earth." (Aristotle, On the heavens, Book II, part 14)
2.5 The Weird Argument from Motion.
"The lowest place belongs to the heaviest and lowest of bodies. The Earth is the heaviest body. The center of the world [universe] is the lowest place. Thus Earth lies at the center of the world. ... If Earth were shifted towards the moon, heavy bodies would still tend toward the center of the world, not towards the Earth. (So if the sun were at the center of the world, all heavy objects would naturally fall toward the sun, which is contrary to experience.) (Summarized by Graney in "126 Arguments Concerning the Motion of the Earth.")
IOW, all the empirical evidence seemed to be against a mobile earth and in favor of a stationary earth.2.6 The Argument from Heavenly Motions.
"We see with our senses the sun and moon and many stars rise and set from day to day, and some stars turn around the arctic pole. This could not be except by the movement of the heavens." (Oresme, "On the book of the heavens and the world by Aristotle.")
So what were the arguments in favor of geomobility?
3. Mystical Woo-woo
But… didn’t Aristarchus and the Pythagoreans propose heliocentrism in ancient times? If only they had prevailed, we might have had Real Science™ millennia sooner! We'd be on freaking Mars by now! What was their evidence?Well, you see, Fire is nobler than earth and the center is a nobler position. So fire has to be in the center. QED.
 |
| Da Man |
There are many names for this sort of thinking, but “scientific” is not one of them. Aristotle says of the Pythagoreans:
In all this they are not seeking for theories and causes to account for observed facts, but rather forcing their observations and trying to accommodate them to certain theories and opinions of their own.Today, we have answers to the objections listed above, many of them developed in the Middle Ages; but those answers depend on the most part on measurements and concepts that were not then available: force, mass, inertia, etc. For example, Oresme answered the Argument of the Winds by postulating common motion: the sphere of the air is also moving to the east along with the sphere of the earth. But he had no propter quid to explain why the air and the earth shared a common motion. You can't just say that if only A and B were true, then observation C would follow. You actually have to show that A and B are true. The Pope said as much to Galileo, and got mocked for his pains.
– Aristotle, On the heavens II.13.293a
Oresme did undermine the one positive argument for a stationary earth when he appealed to relativity:
In the fourth book of The Perspective of Witelo, [he says] that one can perceive movement only in such a way as one perceives one body to be differently disposed in comparison with another. I say, then, that if the lower of the two parts of the cosmos ... should today move with a diurnal movements while the upper (that is, the heavens) should not, we could not perceive this change in any way, but everything would seem the same today and tomorrow. It would seem to us continually that the part where we are situated was at rest and that the other part was always moved, just as it seems to a person who is in a moving ship that the trees outside are moved. Similarly, if a person were in the heavens and it were posited that they were moved with a diurnal movement, and [furthermore] that this man who is transported with the heaven could see the earth clearly and distinctly and its mountains, valleys, rivers, towns, and chateaux, it would seem to him that the earth was moved with a diurnal movement, just as it seems to us on the earth that the heavens move. Similarly, if the earth and not the heavens were moved with a diurnal movement, it would seem to us that the earth was at rest and the heavens moved. This can be imagined easily by anyone with good intelligence. For this [reasoning] is evident the response to the [apparent motion of the heavens], since one could say that the sun and the stars appear thus to set and rise and the heavens to turn as the result of the movement of earth and its elements where we are situated.In short, motion is relative to the inertial reference frame in which the observer is situated. Oh, them unscientific medieval dark agers!
There were similar rebuttals to most of the arguments: plausible-sounding but unevidenced. The most serious objections were those dealing with Coriolis-like effects and with parallax.
The Copernicans answered the Argument from Parallax by claiming that the stars are much farther away and the parallax is therefore too small to detect. But you cannot save one unproven hypothesis by adding a second unproven hypothesis to it, and there were sound scientific reasons for supposing the stars to be closer.
4. Another Fine Math You've Gotten Us Into -- the 1500s
In the question of mobile vs. stationary earth, you have a 50/50 chance of guessing right. But if science were no more than lucky guesses, we’d credit Jonathon Swift with discovering the moons of Mars. There were only two practical reasons for studying the heavens:- to prepare calendars and
- to cast horoscopes.
One wee problem. It conflicted with Aristotelian physics.
You see, the Ptolemaic model was not strictly geocentric. Each planet was embedded in an orb made of dark matter (aether) which carried it along a circular path called a deferent.
- To account for the changes in speed that we now associate with Kepler’s equal area law, the deferent was centered not on the Earth but on a point halfway between the Earth and an imaginary locus called an equant.
- To account for retrograde motion and changes in size and brightness, planets moved on a second circle called an epicycle riding along the deferent.
 |
| Fig. 6. Reading the orbituary. The deferent is to account for changes in speed. The epicycle is to account for retrograde motion and changes in size and brightness. |
These mathematical devices really, really bugged the physicists. In Aristotelian physics all the orbs are homocentric on the Earth. The orbs were like nested ball bearings made of aether, which carried the planets within them. There was no room for such foo-foo as epicycles; and no philosophical justification for the @#$%* equants! (Æther -- from aei thein: "always running" -- also explains why the Michelson-Morley experiment failed. Earth doesn't fly through the aether; it is carried along within it.)
The astronomers’ only excuse was that their calculations worked. The physicists groused, “Sure, in practice, but do they work in theory?”
There was only one solution.
5. Astronomy is not Physics
More than any other unexamined assumption, this one startles us moderns. Except for the Sun and Moon, inexplicably of the same apparent size, the planets and other stars are little more than dots in the sky. "We sense little of the heavens," said Aristotle, except luminous stars and planets, and perceive none of their properly sensible attributes (color, smell, sound) and even the common sensibles (magnitude and motion) are difficult to sense without the propers. (De Anima, 2.6) |
| Andy Osiander commits the crime of being actually correct |
"The suppositions that these astronomers have invented need not necessarily be true; for perhaps the phenomena of the stars are explicable on some other plan not yet discovered by men."Anticipating Duhem and Quine, Thomas also noted the underdetermination of science regarding astronomical models:
-- De coelo, II, lect. 17
“The theory of eccentrics and epicycles is considered as established because thereby the sensible appearances of the heavenly movements can be explained; not, however, as if this proof were sufficient, forasmuch as some other theory might explain them.”Copernicus would later supply "some other theory" to explain the same appearances. Too bad he wasn't around a couple hundred years earlier.
– Summa theologica, I, q.32, a.1, ad. 2
6. The Return of Mystical Woo-woo -- the 1530s
Ptolemy's math worked fine for a thousand years. It was "settled science," as we say today. But gradually, as the star tables were copied and recopied, copyist errors crept in and multiplied like loaves and fishes. This was not due to bugs in the Ptolemaic model, but to errors in the data itself.The Italian Renaissance was a humanist reaction against Aristotelian obsessions with logic, reason, and natural philosophy. Greco-Roman art and literature were “rediscovered.” Platonic mysticism was revived, along with astrology, magic, Hermeticism, and Pythagoreanism. Natural science faltered*; but since astronomy was only mathematics, it prospered.
(*) faltered. Did someone say 'DaVinci'? He was an artisan engineer.
You need more than sketches for SF cover art to be a scientist.
You need more than sketches for SF cover art to be a scientist.
In particular, the humanists were unhappy with the Earth's position in the scheme of things. She was in the bottom of the world, farther from Heaven than anything but Hell itself. Hell was situated in the center of the Earth, which was assumed therefore to be incredibly hot. The humanists wanted to raise the position of the Earth (and hence, of humans) by elevating her into the heavens. Since the Ptolemaic system was beginning to falter from those accumulative copyist errors, they decided to make fresh new accurate observations of the heavens.
Ha-ha. TOF is joking, of course. They were humanists! No, they decided instead to turn the entire universe inside out.
 |
| Nicky Kopernick |
Cardinal Nicolaus von Schönberg and Bishop Giese urged him to publish, but he had already been satirized on the stage and dreaded the mockery of those who “on account of their natural stupidity hold the position among philosophers as drones among bees.”(*) De revolutionibus caused great excitement among mathematicians when it appeared. However, the enthusiasm quickly dried up; and for a reason that startles us Moderns.
(*) drones among bees. From the Dedication of De revolutionibus.
The Renaissance replaced the syllogism with the witty insult.
The Renaissance replaced the syllogism with the witty insult.
The new system was no improvement.
7. The Copernican Flop
It’s not enough for a new model to equal the standard model in predicting phenomena; it must do better. Otherwise, why bother changing? And the Copernican model did not do that. Nor were its calculations simpler. To preserve pure Platonic circles, Copernicus used twice as many epicycles as Peuerbach’s then-current edition of Ptolemy! That's right: epicycles. The Earth revolved around the Sun on two circles; the Moon ran on an unprecedented double epicycle, and Mercury librated idiosyncratically across the center of an epicycle! Try explaining that with a theory of universal gravitation!Technically, Copernicanism wasn’t even heliocentric: The Sun was off-center, and planetary motions were referenced to the center of the Earth’s orbit instead. And because each planet was solved as a separate problem, each planet orbits a different center!
There were two reasons for the epic fail of the Copernican model:
- Copernicus insisted on pure Platonic circles; and
- Accumulated copyist errors in the Alfonsine Tables carried into his Prussian Tables.
8. Enter Tycho Brahe -- 1570s
 |
| Tycho Brahe, Imperial Mathematician |
 |
| Tycho's "mural quadrant" |
And produced a geo-heliocentric system regarded today as a kludge.
How could the greatest astronomer of his age be so stoopid?
 |
| Fig. 8. Tycho's updated Heraclidean model. |
- Procyon has the same diameter and brightness as Saturn.
- If Procyon is much farther than (say) 100 times Saturn’s distance, simple geometry proves its actual size would dwarf the sun.
- All the stars would dwarf the Sun, which would then be the only pea in a universe of melons, which is absurd.
- But if Procyon were any closer, there would be visible parallax from the Earth's revolution.
- There is no visible parallax.
- Lack of parallax plus the apparent size of the stars therefore requires a stationary Earth. QED.
 |
| Fig. 9. Geometric optics. The farther an object is, the bigger it must be to present a disk of a given size. |
Did anyone notice the pea under the thimble? Go ahead, think on't. TOF will wait.
Because Tycho otherwise admired Copernicus’ treatment but empirical data and solid science forced him to conclude that the Earth was stationary, his solution was an updated Heraclidean model: all planets circling the Sun, but the Sun and Moon circling the Earth!
The Imperial Mathematician, Nicolai Reymers Bär, styled “Ursus,” proposed a similar model – but with a rotating Earth. Tycho accused him of plagiarizing his data and a feud developed that caught a young math teacher named Johann Kepler smack in the middle.
Like many new authors, Kepler had sent copies of his book (Mysterium Cosmographicum, “a strange Renaissance piece of Platonic Pythagorean mathematical mysticism”) to famous people, including Tycho and Ursus, hoping for blurbs. Ursus used Kepler’s thank-you note to make it seem that Kepler favored the Ursine over the Tychonic model. Since Kepler was asking Tycho for a job at the time, this caused some embarrassment.
Kepler also received an unsolicited fan letter from an unknown math professor at Padua who had got hold of a copy of the book, and whose name amused Kepler. His forename and family name are the same! Kepler wrote to a friend. “Galileus Galileus.” In Italian, Galileo Galilei.Tycho's great kludge was thus the best model that accounted for the data. Further, it was mathematically equivalent to the Copernican model. Anything the one model could do the other model could do as well. Even today, however, there are those who believe that Tycho was living in fear of the all-powerful Church -- even though he lived in Lutheran Denmark and had the favor of the king, who showered money on his Uraniborg observatory proportionate to the kingdom's budget as NASA was to the US budget. After he and the king quarreled, Tycho moved to Prague, where the Catholic Emperor made him Imperial Mathematician, succeeding Ursus. He died of a burst bladder in...
Hey! Wait a gol-danged minute! (TOF hears you say) Procyon doesn't have a disk!
9. Airy Abstractions: a brief excursion into the future
That's right. The apparent disks of the stars are caused by the diffraction pattern resulting from a uniformly-illuminated circular aperture. The bright region in the center is known as the Airy disk, not because they are caused by the air, but because they were identified and studied by George Biddell Airy......In 1835. So we can't blame ol' Tycho for not realizing that the diameters of stars were optical illusions. In an 1828 article for Encyclopedia Metropolitana, astronomer John Herschel described the appearance of a bright star seen through a telescope under high magnification:
 |
| Fig. 10. Herschel's star. Even with 19th cent. telescopes, stars appeared as disks. |
...the star is then seen (in favourable circumstances of tranquil atmosphere, uniform temperature, &c.) as a perfectly round, well-defined planetary disc, surrounded by two, three, or more alternately dark and bright rings, which, if examined attentively, are seen to be slightly coloured at their borders. They succeed each other nearly at equal intervals round the central disc....Once the illusory nature of Airy disks was realized, the stars could be as distant as you might like. Their diameters were not real and implied nothing about their sizes. But no one will know this for another quarter millennium.
10. The Last Hurrah of Eyeball Astronomy -- the 1600s
 |
| Johnny Kepler cleaning his fingernails with a compass |
Remember, Nick was using bad data. He had made very few actual observations and was simply reworking published tables. Tycho was able to show with his pristine and precise new data that the “trepidations of the equinoxes” was simply observational error.
Now for the orbit of Mars, which Nicky had really messed up. The sucker was way out of position; so either Copernicus was wrong (falsified) or Mars was wrong. Tycho hired Kepler to fix the orbit of Mars; though, remembering Ursus, he would not allow Kepler to make copies of the double-plus Secret Data of Uraniborg. He had to use them on-site. But in 1601, Kepler succeeded Tycho as Imperial Mathematician, and negotiated better access to the data with Longomontanus, Tycho’s heir and long-time assistant.
 |
| Johnny Kepler computes Mars using Copernicus, Ptolemy, and Tycho |
A Neoplatonic mystic, Kepler was convinced that physics must reduce to simple mathematical forms, but he was more liberal than either Copernicus or Galileo. He began to try ovals.
This bugged Longomontanus, who accused Kepler of shoveling shit and gave the world a colorful phrase to replace "your argument is lacking in merit." In a letter of 6 May 1604, he told Kepler he was "submerged in shit in the Augean stable of old…" Kepler replied in early 1605:
If you are angry that I cannot eliminate the oval path, how much more ought you to be angry with the spirals [epicycles], which I abolished. … This is like being punished for leaving behind one barrow full of shit although I have cleaned the rest of the Augean stables.Scientists have been accusing one another of shoveling it ever since.
The mathematical difficulty of generating ovals had led Kepler to complain earlier that year (4 July 1603) to David Fabricius: “I lack something: knowledge of the geometrical generation of the oval path … If the figure were a perfect ellipse…!”
Yeah, if only.
Kepler decided to chuck two basics of physics:
- the motion of heavenly bodies is uniform
- the motion of heavenly bodies is circular
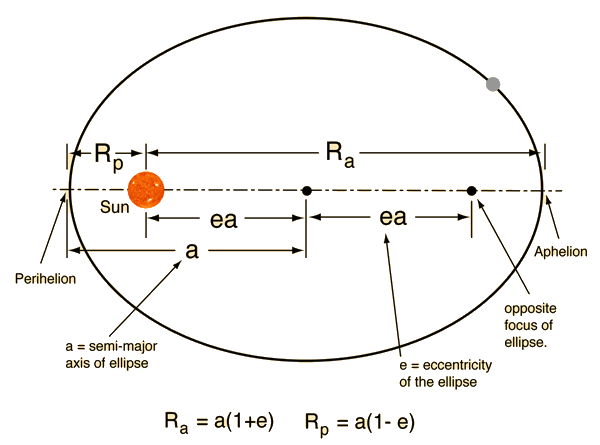 |
| Fig. 11. An elliptical comment. |
In 1604 he gave up Platonic circles.
He was able to show geometrically that movement along an ellipse was mathematically equivalent to movement along an epicycle on a deferent. Shazaam! – the Martian orbit suddenly made sense! And btw, the other focus of the ellipse does kinda sorta look like that @#$^&;% equant...
Without Tycho’s precise new data, Kepler would never have found his ellipse. No one before Tycho could possibly have done so. The old tables were just too badly corrupted. The interesting corollary to this is that as soon as it was possible to do so, European astronomers discovered elliptical orbits.
 | |
| Johnny Kepler's best seller, not. |

Game, set, and match, dudes and dudettes! (insert glyph of victory dance→→→) Kepler had the correct mathematical answer before the telescope was invented. Hear the applause?
That's the sound of one hand clapping while a tree falls in the forest. In later years, Kepler will admit ruefully that he tried to read his own book once and couldn't make heads or tails out of it. As a writer, his scintillating prose can be summarized as "WTF?"
Besides, Kepler had only Platonic number mysticism to back himself up. He had neither empirical evidence nor physical theory that his model was physically true. It predicted the heavens; but then, so did the Ursine/Tychonic system. And the latter explained the lack of parallax and Coriolis directly, without making additional assumptions.
Kepler sent a copy of Astronomia nova to Galileo – but Galileo never read it.
Denoument
So what happened next? (TOF hears you ask).A troll and glory hog named Galileo swooped in, claimed credit for everything in sight, and delayed acceptance of heliocentrism for the rest of his lifetime. But that is a story for another time; viz.,
Bibliography
Aristotle. On the Heavens.Christie, Thony. But it doesn’t move! June 22, 2011.
Copernicus, Nicholas; Charles Wallis (trans). On the Revolutions of the Heavenly Spheres.
Crombie, A. C. Medieval and Early Modern Science, vol. II. Garden City, NU: Doubleday Anchor, 1959.
Flynn, Michael. The Great Ptolemaic Smackdown and Down 'n Dirty Mud Wrassle. Analog (Jan/Feb 2013)
Franklin, James. "The Renaissance Myth" Quadrant 26 (11) (Nov. 1982), pp. 51-60
Graney, Christopher M. 126 Arguments Concerning the Motion of the Earth. Mar. 14, 2011.
—. Tycho was a scientist, not a blunderer. Mar. 6, 2012.
Oresme, Nicholas. On the Book of the Heavens and the World by Aristotle. Feb. 1999.
Osiander, Andreas. Foreword to Copernicus' Revolutionibus. unsigned.
Ptolemy, Claudius. Syntaxis Mathematiké. In The Great Books Series. Chicago: Encyclopedia Britannica/Univ. of Chicago, 1952.
Thomas Aquinas. De coelo, II, lect. 17
—. Summa theologica, I, q.32, a.1, ad. 2
Wikipedia. Airy disks and patterns.





Any significance to Archimedes' using a heliocentric model to figure the size of the universe? (http://en.wikipedia.org/wiki/The_Sand_Reckoner)
ReplyDeleteDoes this suggest that such a theory/model was accepted in his day and place?
Archimedes did not accept the Aristarchian notion. He only uses it in The Sand Reckoner to get the largest possible figure for the size of the kosmos. For example, he writes (Book II, 17-18):
Deletehttp://www.calstatela.edu/faculty/hmendel/Ancient%20Mathematics/Archimedes/SandReckoner/SandReckoner.html
For since it is supposed that the earth has the same ratio to the world as described by us which the described world has to the sphere of the fixed stars which Aristarchus supposes, i.e., the diameters of the spheres have the same ratio to one another, but the diameter of the world has been proved to be smaller than ten-thousand-times the diameter of the earth, it is thus clear that the diameter of the sphere of the fixed stars is smaller than ten-thousand times the diameter of the world. {You will note he contrasts the two systems - TOF]
But since spheres have to one another the triplicate ratio of their diameters, it is obvious that the sphere of the fixed stars which Aristarchus supposes is smaller than the world multiplied by ten-thousand-times ten-thousand myriads.
In fsct, he always uses the phrase "Aristarchus supposes." Also of interest, it is only through The Sand Reckoner that we even know that Aristarchus held this theory. His only extant work makes no mention of it.
that passage doesn't seem to have anything really to do with heliocentrism... I like these blog posts but maybe you could go in depth about Archimedes' relation to heliocentrism.I don't see where Archimedes really compares the heliocentric and geocentric models. Also of note for you is the comment by Hungarian-Jewish mathematician George Polya, who states in his book Mathematical Methods In Modern Science that Aristarchus' proofs were weak.
DeleteArchimedes did not seem to take the Pythagoreans seriously enough to argue one vs. the other. The falsity of heliocentrism was obvious from the lack of visible parallax plus the distances deduced from their brightness and diameter. Polya could not have meant Aristarchus' proofs of heliocentrism, since none have come down to us. (We only know that Aristarchus held the Sun in the center because Archimedes mentioned it in "The Sand Reckoner.")
DeleteI'm really glad to have a chance to read this - the small segments you've done on this topic were fascinating, and it's nice to see an entire post dedicated to the topic.
ReplyDeleteTo be totally fair to Kepler, it would seem that he had good math intuition. He just had trouble with the bit where you find facts and numbers and theory to back up your gut understanding.
ReplyDeleteHaving the right answer for the wrong reason is similar to doing the right thing for the wrong reason -- it's usually good in the short term, but in the long term it can really mess you up. Still, intuition is a very good thing for surviving long enough to discover your mistakes in reasoning.
A troll and glory hog named Galileo swooped in, claimed credit for everything in sight, and delayed acceptance of heliocentrism for the rest of his lifetime.
ReplyDeleteKind of overstated, would you not say? I will be waiting for your arguments, but I would remind you that the real scientific revolution takes place when people gain enough justified assurance in the scientific method of investigation as to take its results, once properly proved, for granted. Galileo was the first person to show this confidence, to the extent that he could not bring himself to give, as he had been required, a fair shake to theories he regarded as mistaken, as compared to theories he regarded as correct. As I recall, this, rather than teaching the heliocentric theory, was what he was condemned for. His opponents resented his certainty because they still lived in the world of ideas of Aristotle and Thomas Aquinas, in which astronomical theories are not certain and may be no more correct than others now insufficiently worked out or even unknown. The claim of truth to facts which Galileo makes and backs up with experimental evidence is the real step forwards.
No one had trouble with Galileo's science. It was that a) the actual facts seemed against him and b) he was insisting on how to read scripture properly at the same time.
DeleteHis opponents resented his certainty because they still lived in the world of ideas of Aristotle and Thomas Aquinas, in which astronomical theories are not certain and may be no more correct than others now insufficiently worked out or even unknown.
DeleteThat is, in fact, the case — always. Scientific theories, in astronomy or out of it, are always underdetermined: any given body of facts can be accounted for equally well by multiple theories and multiple mathematical constructs. And there are always new data, and phenomena previously undiscovered, which require refinement and revision of even the most apparently incontestable theory. What you are saying, in effect, is that Galileo made a claim of epistemic certainty that natural science of its nature ought not to make and cannot defend.
The claim of truth to facts which Galileo makes and backs up with experimental evidence is the real step forwards.
But he had no experimental evidence. Every bit of evidence he offered in support of the heliocentric hypothesis was equally well accounted for by the Tychonic system. And some of the evidence was entirely bogus: for instance, his using the diurnal tides as proof that the earth rotates on its axis. He had never heard of semidiurnal tides, and when he was corrected on this point, he ignored it and continued to maintain his previous position. Further, he never offered any explanation of how a uniform rotary motion could lead to the periodic and non-uniform phenomenon of the tides.
If you want a real step forwards in astronomy, look to Tycho Brahe, who threw out the error-riddled astronomical tables of his day, built his own instruments, and dedicated his whole life to making accurate observations of the sky. Or to Kepler, who threw out the preconception of uniform circular motion and (after many false starts and blind alleys) discovered a mathematical formalism that actually did account for the motions of the planets as described in Tycho’s improved data. Or to Newton, who developed an entire new branch of mathematics in order to find a sound theoretical basis for Kepler’s formalism, and in the process, established that heavenly bodies were subject to the same laws of motion as earthly ones, and that astronomy could, in fact, be regarded as a branch of physics.
Curiously, nobody questions the principle of mediocrity that lies at the base of Big Bang and other cosmological speculations.
ReplyDeleteHowever, this principle is not empirical but expresses an aesthetic preference.
So how would an empiricist justify Big bang and cosmic expansion as a fact?
Good question. Seems modern celebrity Catholics are okay with atheist assumptions, yet do everything in their power to mock fellow Catholics. What they are really doing is out of fear of losing their privileged standing. They are afraid of rocking the boat and be considered foolish in the eyes of the world.
Delete1. The principle of mediocrity does not underlie the "Big Bang" solution to the relativistic field equations.
Delete1.1 "Mediocrity" was, from the point of view of the medievals, a big promotion in the Earth's status. They had regarded the Earth as in the lowest and most ignoble position, at the bottom of the world.
1.2 The equation of the "center" with the "noble" was a pagan assumption.
2. The name "Big Bang" was first applied to Msgr. Lemaitre's solution by the atheist Fred Hoyle in mockery of a theory he saw as too 'creation'-like.
3. Expansion is an empirical observation, and was predicted by Msgr. Lemaitre on the basis of his solution to the field equations, later borne out telescopically by Hubble.
4. The "principle of mediocrity" is indeed not itself a scientific principle. More importantly, it is not even a philosophical principle.
In other venues, Mr. Flynn, you've appealed to the Medieval proof of the speed of sound being slower than light as a kind of proto-experiment --- "you see the hammer hit before you hear the clang." Because it is medieval, it is, so the claim goes, it is proof that science was born in the High Middle Ages.
ReplyDeleteHowever, in this article you list several proofs which seem similar to that Medieval test, appealing as it does to popular experience. One of two things seems clear. Either:
1. These statements are also medieval in origin, or
2. "Proto-science" of the kind you've mentioned is not unique to the Middle Ages.
Also, Mr. Flynn, I thought you might appreciate this blurb about Riccoli ---
ReplyDeletehttp://www.newscientist.com/article/dn19979-coriolislike-effect-found-184-years-before-coriolis.html#.UhuCfRtwo-c
Perhaps I am confused, but it appears to me that the diagram labeled Figure 4 is incorrect? With the world turning "to the right" as depicted then the flight of the object would be a parabola in the oposite direction as it were. Unless my imagination fails me?
ReplyDeleteAh, I posted too soon. After further contemplation the figure is indeed correct! I should have assumed as much - I have yet to catch TOF in an error.
DeleteRight. The Argument from Coriolis is that the object at the top of the tower will have an eastward velocity relative to the base.
DeleteThank you for reproducing this article here. The essay in Analog is probably my favorite of your articles, both in terms of enlightenment and of good ol' entertaining reading. I really want to make a bunch of copies of it and shove it at anyone who repeats the Galileo myth.
ReplyDeleteCan I ask you about the source of this comment: "The suppositions that these astronomers have invented need not necessarily be true; for perhaps the phenomena of the stars are explicable on some other plan not yet discovered by men."
ReplyDelete-- De coelo, II, lect. 17
In the link to the De Caelo provided, the quotation appears as:
"Yet it is not necessary that the various suppositions which they hit upon be true - for although these suppositions save the appearances, we are nevertheless not obliged to say that these suppositions are true, because perhaps theme is some other way men have not yet grasped by which the things which appear as to the stars are saved. "
Which is not as elegant. Do you have an alternate translation?
Illorum tamen suppositiones quas adinvenerunt, non est necessarium esse veras: licet enim, talibus suppositionibus factis, apparentia salvarentur, non tamen oportet dicere has suppositiones esse veras; quia forte secundum aliquem alium modum, nondum ab hominibus comprehensum, apparentia circa stellas salvantur.
Deletehttp://www.corpusthomisticum.org/ccm2.html
Nice post. I do take issue with this remark, near the beginning:
ReplyDeleteA century, more-or-less, is generally what it takes for quantum mechanics, general relativity, and sundry other theories to progress from "wild hypothesis overthrowing the wisdom of the ages" to "standard model,"
Now, what does "more-or-less" mean? GR appears fully formed on the scene in 1915, QM in 1925. Einstein's first attempt to reconcile gravitation with relativity was published in 1907, and Planck's famous blackbody law dates from 1900.
GR was notoriously difficult to subject to experimental tests; even so, Clifford Will's Was Einstein Right? Putting General Relativity To The Test makes it clear that it was solidly established by the late 1970s at the absolute latest. If we look at, say James Jeans' The Universe Around Us (3rd ed., 1933), we find endorsements like, "The general theory of relativity has long passed the stage of being regarded as an interesting speculation. It has accounted for phenomena of planetary motion which Newton’s law of gravitation had entirely failed to explain..."
As for QM, this became standard physics much faster. As just one indicator, consider the famously conservative Nobel committee and the key physics prizes for QM: Planck, 1918, Bohr, 1922, de Broglie, 1929, Heisenberg, 1932, Schrödinger and Dirac, 1933. And those are just the theoretical prizes.
Stretching things to the utmost, one could claim that QM took around 35 years to become standard physics. A more reasonable figure would be around 10 (1925 to 1935). As for GR, maybe 70 at the outside, or more reasonably 40 to 50.
One last question: given the enormous variety of historical circumstances at play, why is a general "100 years" rule even plausible?
Alates 1980-ndast aastast (mul on alles kirjavahetus NL Teaduste Akadeemia Presiidiumi Esimehega!) olen "raiunud kui rauda":
DeleteGalilei teisendused: x´= x - vt; y´= ky; (k = 1/L, milles L - on nn. Lorentz-tegur).
70-ndail näidati "Terrell pööre" - et "pikkuste kontraktsioon - on illusioon".
MIKS me ei usu Galileo Galileid?
I completely agree, and in fact I would say that at least by the first Solvay conference in 1911, quantum mechanics had been widely accepted among researchers as an important part of fundamental physics. If you want to be more conservative, the fifth conference, in 1927, didn't leave much room for doubt.
DeleteThe other way the period could be stretched out is by moving the first-serious-proposal date. I don't know of anything before the dates you give for general relativity and QM, but special relativity had a pre-Einsteinian 'prequel' that is not mentioned in simple accounts, in the work of FitzGerald, Lorentz, Poincare, Larmor and even Heaviside. Even with that, special relativity was not much more than fifteen years in the making.
Newtonian mechanics was accepted pretty quickly, and also Maxwell's electrodynamics. Darwin's evolution was scientifically accepted in a few decades, even if we include his delay in publishing. The only century-long post-Galilean acceptance process that I can think of offhand was that of atomic theory, if we take Dalton as the originator of the first not-simply-speculation form of the theory. That process seems to have been delayed by excessive deference to philosophical speculation about how things ought to be, and you might say the same about geocentrism, if you consider theology to be a sort of philosophy.
Sisuline lahendus (osaliselt) on
ReplyDeleteTõnu:veebiruum
Hi Mike - congratulations on a great blog series. We've written a little piece about it: http://www.catholicculture.org/commentary/the-city-gates.cfm?ID=709
ReplyDeleteKepler wrote this up in Astronomia nova (1609). Since he believed mathematics caused physics, he decided that there must be a universal cause of planetary motions: the Sun projected a field, which by rotating would chivvy the planets around their ellipses with an impetus inversely proportional to their distance. Okay, you can’t get everything right; but this prepared the way for Newton. Kepler thought the field was the Holy Spirit, which proceeded from the Father (the Sun) toward the Son (the fixed stars). This did not prepare the way for Newton.
ReplyDeleteYou might be surprised. Newton saw himself as a theologian first and foremost, and believed the most important application of his discoveries in physics and math were to demonstrate the glory of God made manifest in the word around us.
Actually, general relativity and quantum mechanics were given respectful notice almost immediately, and became generally accepted well within the working lifetime of those who discovered them. The 19th-century neo-Newtonian synthesis collapsed almost overnight from the 1880's on.
ReplyDeleteKuhn got it completely wrong.
Physicists tend to value the mathematical elegance of theories because long experience has shown that there's a definite tendency for this to indicate truth.
ReplyDeleteMy apologies, I thought "You-Know-Who" was Lord Voldemort.
ReplyDeleteThanks so much, Mr. TOF, for this exquisitely interesting and carefully considered article. It is my predisposition, as it seems to be yours, to think it is more fruitful to understand the real reason ideas were what they were at the time they were mainstream, then to comfortably recast current ideas as a progression of refinements to something that originated when supposedly, around 1600, civilization at last got smart. Or, reality is more interesting to me than hype.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDeleteCool. But does not compute, does it:
ReplyDelete"Did someone say 'DaVinci'? He was an artisan engineer.
You need more than sketches for SF cover art to be a scientist."
You're basically making him a nutty ancient as well.
I also don't know enough about the specifics and context, but the following does seem straightforwardly contradictory with the whole section 5 or the Aquinas quotation therein:
" You can't just say that if only A and B were true, then observation C would follow. You actually have to show that A and B are true. The Pope said as much to Galileo, and got mocked for his pains."
Otherwise remarkable and refreshing.
For explication, I interpret that last quotation based on another information about that "mocking" of the pope that sounds more similar to Aquinas and the explanation of pheonomena than a simple reminder of "evidence".
DeleteHere'sanother thought: Kopernicans might have been guided by an observational instinct not based on precise measurements but still a relatively higher simplicity or order than a Ptolemaic model... I haven't hought into this much, it's just the attempt of a formulation of something which I have in hte back of my mind when I read certain historico-"relativistic" accounts...
ReplyDeleteVery Good Stuff.
ReplyDeleteJust a question:
In later years, Kepler will admit ruefully that he tried to read his own book once and couldn't make heads or tails out of it. As a writer, his scintillating prose can be summarized as "WTF?"
I'm curious, what was Kepler's exact statement on his own work? I can't find this anecdote.
The pictures, the pictures are going missing! :O
ReplyDeleteTOF! Your image links are breaking! I still share this series with new readers.
DeleteThis comment has been removed by a blog administrator.
ReplyDeleteIt seems your friend Mark Shea is rerunning this on his blog today.
ReplyDeleteAs to its being 6021:st anniversary of the Universe, like he says, in the times of Father Martino Martini, SJ, the Ussher chronology was considered an innovation. It was popular among Catholics because it agrees with the Vulgate, while the Roman Martyrology does not. But as it was an innovation and in conflict with Roman Martyrology, it could not be canonised.
He took a cue from Chinese history as saying it worked totally well with LXX (supposing the Chinese came there before Babel), and not too bad with Roman Martyrology (indeed, if the 2952 BC for Fu Xi beginning his reign is taken as in Roman Martyrology, rather than either preferring Syncellus' version of LXX or considering that Chinese chronology inflated, then Fu Xi would need to be a son or grandson of Noah - like Ham setting up a "summer house" in China or some grandson of Noah getting born).
If you have any desire to see my own take on this (close enough to Father Martini's, Jesuit friend as I am, previous to Settele or so), [click - > ] here is my own post [ < - click]
Oh, btw, since Mark Shea also finished the rerun by a diatribe against "greatest Catholics of all times" "anointed to defend the Church from Pope and Magisterium", I made [click - > ] another post [ < - click] with some comments on how Bergoglio's words from 2014 fare if compared to Pius XII supposing he was Pope and Humani Generis, supposing it was Magisterium.
DeleteCouldn't finish this because of all the clown talk.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDeleteIt seems that Tycho was (almost) right, after all... www.tychos.info
ReplyDeleteIf you mean, he omitted elliptic orbits, this was corrected by Riccioli.
DeleteOops, seems we deal with someone who thinks Earth is orbitting within a Sun-Mars binary system ....?
DeleteThis comment has been removed by a blog administrator.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDeleteMalatya
ReplyDeleteKırıkkale
Aksaray
Bitlis
Manisa
X1E
Afyon
ReplyDeleteAntalya
Erzurum
Mersin
izmir
Z2SPN